Boy or Girl paradox
The Boy or Girl paradox surrounds a well-known set of questions in probability theory which are also known as The Two Child Problem,[1] Mr. Smith's Children[2] and the Mrs. Smith Problem. The initial formulation of the question dates back to at least 1959, when Martin Gardner published one of the earliest variants of the paradox in Scientific American. Titled The Two Children Problem, he phrased the paradox as follows:
- Mr. Jones has two children. The older child is a girl. What is the probability that both children are girls?
- Mr. Smith has two children. At least one of them is a boy. What is the probability that both children are boys?
Gardner initially gave the answers 1/2 and 1/3, respectively; but later acknowledged that the second question was ambiguous.[1] Its answer could be 1/2, depending on how you found out that one child was a boy. The ambiguity, depending on the exact wording and possible assumptions, was confirmed by Bar-Hillel and Falk,[3] and Nickerson.[4]
Other variants of this question, with varying degrees of ambiguity, have been recently popularized by Ask Marilyn in Parade Magazine,[5] John Tierney of The New York Times,[6] and Leonard Mlodinow in Drunkard's Walk.[7] One scientific study[2] showed that when identical information was conveyed, but with different partially-ambiguous wordings that emphasized different points, that the percentage of MBA students who answered 1/2 changed from 85% to 39%.
The paradox has frequently stimulated a great deal of controversy.[4] Many people argued strongly for both sides with a great deal of confidence, sometimes showing disdain for those who took the opposing view. The paradox stems from whether the problem setup is similar for the two questions.[2][7] The intuitive answer is 1/2.[2] This answer is intuitive if the question leads the reader to believe that there are two equally likely possibilities for the sex of the second child (i.e., boy and girl),[2][8] and that the probability of these outcomes is absolute, not conditional.[9]
Contents |
Common assumptions
The two possible answers share a number of assumptions. First, it is assumed that the space of all possible events can be easily enumerated, providing an extensional definition of outcomes: {BB, BG, GB, GG}.[10] This notation indicates that there are four possible combinations of children, labeling boys B and girls G, and using the first letter to represent the older child. Second, it is assumed that these outcomes are equally probable.[10] This implies the following model, a Bernoulli process with 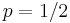 :
:
- Each child is either male or female.
- Each child has the same chance of being male as of being female.
- The sex of each child is independent of the sex of the other.
In reality, this is an incomplete model,[10] since it ignores (amongst other factors) the fact that the ratio of boys to girls is not exactly 50:50, the possibility of identical twins (who are always the same sex), and the possibility of an intersex child. However, this problem is about probability and not biology. The mathematical outcome would be the same if it were phrased in terms of a gold coin and a silver coin.
First question
- Mr. Jones has two children. The older child is a girl. What is the probability that both children are girls?
Under the forementioned assumptions, in this problem, a random family is selected. In this sample space, there are four equally probable events:
| Older child | Younger child |
|---|---|
| Girl | Girl |
| Girl | Boy |
Only two of these possible events meet the criteria specified in the question (e.g., GG, GB). Since both of the two possibilities in the new sample space {GG, GB} are equally likely, and only one of the two, GG, includes two girls, the probability that the younger child is also a girl is 1/2.
Second question
- Mr. Smith has two children. At least one of them is a boy. What is the probability that both children are boys?
This question is identical to question one, except that instead of specifying that the older child is a boy, it is specified that at least one of them is a boy. In response to reader criticism of the question posed in 1959, Gardner agreed that a precise formulation of the question is critical to getting different answers for question 1 and 2. Specifically, Gardner argued that a "failure to specify the randomizing procedure" could lead readers to interpret the question in two distinct ways:
- From all families with two children, at least one of whom is a boy, a family is chosen at random. This would yield the answer of 1/3.
- From all families with two children, one child is selected at random, and the sex of that child is specified. This would yield an answer of 1/2.[3][4]
Grinstead and Snell argue that the question is ambiguous in much the same way Gardner did.[11]
For example, if you see the children in the garden, you may see a boy. The other child may be hidden behind a tree. In this case, the statement is equivalent to the second (the child that you can see is a boy). The first statement does not match as one case is one boy, one girl. Then the girl may be visible. (The first statement says that it can be either.)
While it is certainly true that every possible Mr. Smith has at least one boy - i.e., the condition is necessary - it is not clear that every Mr. Smith with at least one boy is intended. That is, the problem statement does not say that having a boy is a sufficient condition for Mr. Smith to be identified as having a boy this way.
Commenting on Gardner's version of the problem, Bar-Hillel and Falk [3] note that "Mr. Smith, unlike the reader, is presumably aware of the sex of both of his children when making this statement", i.e. that 'I have two children and at least one of them is a boy.' If it is further assumed that Mr Smith would report this fact if it were true then the correct answer is 1/3 as Gardner intended.
Analysis of the ambiguity
If it is assumed that this information was obtained by looking at both children to see if there is at least one boy, the condition is both necessary and sufficient condition. Three of the four equally probable events for a two-child family in the sample space above meet the condition:
| Older child | Younger child |
|---|---|
| Girl | Boy |
| Boy | Girl |
| Boy | Boy |
Thus, if it is assumed that both children were considered while looking for a boy, the answer to question 2 is 1/3. However, if the family was first selected and then a random, true statement was made about the gender of one child (whether or not both were considered), the correct way to calculate the conditional probability is not to count the cases that match. Instead, one must add the probabilities that the condition will be satisfied in each case[11]:
| Older child | Younger child | P(this case) | P("at least one boy" given this case) | P(both this case, and "at least one boy") |
|---|---|---|---|---|
| Girl | Girl | 1/4 | 0 | 0 |
| Girl | Boy | 1/4 | 1/2 | 1/8 |
| Boy | Girl | 1/4 | 1/2 | 1/8 |
| Boy | Boy | 1/4 | 1 | 1/4 |
The answer is found by adding the numbers in the last column wherever you woud have counted that case: (1/4)/(0+1/8+1/8+1/4)=1/2. Note that this is not necessarily the same as reporting the gender of a specific child, although doing so will produce the same result by a different calculation. For instance, if the younger child is picked, the calculation is (1/4)/(0+1/4+0+1/4)=1/2. In general, 1/2 is a better answer any time a Mr. Smith with a boy and a girl could have been identified as having at least one girl.
Variants of the question
Following the popularization of the paradox by Gardner it has been presented and discussed in various forms. The first variant presented by Bar-Hillel & Falk [3] is worded as follows:
- Mr. Smith is the father of two. We meet him walking along the street with a young boy whom he proudly introduces as his son. What is the probability that Mr. Smith’s other child is also a boy?
Bar-Hillel & Falk use this variant to highlight the importance of considering the underlying assumptions. The intuitive answer is 1/2 and, when making the most natural assumptions, this is correct. However, someone may argue that “...before Mr. Smith identifies the boy as his son, we know only that he is either the father of two boys, BB, or of two girls, GG, or of one of each in either birth order, i.e., BG or GB. Assuming again independence and equiprobability, we begin with a probability of 1/4 that Smith is the father of two boys. Discovering that he has at least one boy rules out the event GG. Since the remaining three events were equiprobable, we obtain a probability of 1/3 for BB.”[3]
Bar-Hillel & Falk say that the natural assumption is that Mr Smith selected the child companion at random but, if so, the three combinations of BB, BG and GB are no longer equiprobable. For this to be the case each combination would need to be equally likely to produce a boy companion but it can be seen that in the BB combination a boy companion is guaranteed whereas in the other two combinations this is not the case. When the correct calculations are made, if the walking companion was chosen at random then the probability that the other child is also a boy is 1/2. Bar-Hillel & Falk suggest an alternative scenario. They imagine a culture in which boys are invariably chosen over girls as walking companions. With this assumption the combinations of BB, BG and GB are equally likely to be represented by a boy walking companion and then the probability that the other child is also a boy is 1/3.
In 1991, Marilyn vos Savant responded to a reader who asked her to answer a variant of the Boy or Girl paradox that included beagles.[5] In 1996, she published the question again in a different form. The 1991 and 1996 questions, respectively were phrased:
- A shopkeeper says she has two new baby beagles to show you, but she doesn't know whether they're male, female, or a pair. You tell her that you want only a male, and she telephones the fellow who's giving them a bath. "Is at least one a male?" she asks him. "Yes!" she informs you with a smile. What is the probability that the other one is a male?
- Say that a woman and a man (who are unrelated) each has two children. We know that at least one of the woman's children is a boy and that the man's oldest child is a boy. Can you explain why the chances that the woman has two boys do not equal the chances that the man has two boys?
With regard to the second formulation Vos Savant gave the classic answer that the chances that the woman has two boys are about 1/3 whereas the chances that the man has two boys are about 1/2. In response to reader response that questioned her analysis vos Savant conducted a survey of readers with exactly two children, at least one of which is a boy. Of 17,946 responses, 35.9% reported two boys.[10]
Vos Savant's articles were discussed by Carlton and Stansfield[10] in a 2005 article in The American Statistician. The authors do not discuss the possible ambiguity in the question and conclude that her answer is correct from a mathematical perspective, given the assumptions that the likelihood of a child being a boy or girl is equal, and that the sex of the second child is independent of the first. With regard to her survey they say it "at least validates vos Savant’s correct assertion that the “chances” posed in the original question, though similar-sounding, are different, and that the first probability is certainly nearer to 1 in 3 than to 1 in 2."
Carlton and Stansfield go on to discuss the common assumptions in the Boy or Girl paradox. They demonstrate that in reality male children are actually more likely than female children, and that the sex of the second child is not independent of the sex of the first. The authors conclude that, although the assumptions of the question run counter to observations, the paradox still has pedagogical value, since it "illustrates one of the more intriguing applications of conditional probability."[10] Of course, the actual probability values do not matter; the purpose of the paradox is to demonstrate seemingly contradictory logic, not actual birth rates.
Psychological investigation
From the position of statistical analysis the relevant question is often ambiguous and as such there is no “correct” answer. However, this does not exhaust the boy or girl paradox for it is not necessarily the ambiguity that explains how the intuitive probability is derived. A survey such as vos Savant’s suggests that the majority of people adopt an understanding of Gardner’s problem that if they were consistent would lead them to the 1/3 probability answer but overwhelmingly people intuitively arrive at the 1/2 probability answer. Ambiguity notwithstanding, this makes the problem of interest to psychological researchers who seek to understand how humans estimate probability.
Fox & Levav (2004) used the problem (called the Mr. Smith problem, credited to Gardner, but not worded exactly the same as Gardner's version) to test theories of how people estimate conditional probabilities.[2] In this study, the paradox was posed to participants in two ways:
- "Mr. Smith says: 'I have two children and at least one of them is a boy.' Given this information, what is the probability that the other child is a boy?"
- "Mr. Smith says: 'I have two children and it is not the case that they are both girls.' Given this information, what is the probability that both children are boys?"
The authors argue that the first formulation gives the reader the mistaken impression that there are two possible outcomes for the "other child",[2] whereas the second formulation gives the reader the impression that there are four possible outcomes, of which one has been rejected (resulting in 1/3 being the probability of both children being boys, as there are 3 remaining possible outcomes, only one of which is that both of the children are boys). The study found that 85% of participants answered 1/2 for the first formulation, while only 39% responded that way to the second formulation. The authors argued that the reason people respond differently to this question (along with other similar problems, such as the Monty Hall Problem and the Bertrand's box paradox) is because of the use of naive heuristics that fail to properly define the number of possible outcomes.[2]
References
- ^ a b Martin Gardner (1954). The Second Scientific American Book of Mathematical Puzzles and Diversions. Simon & Schuster. ISBN 978-0226282534..
- ^ a b c d e f g h Craig R. Fox & Jonathan Levav (2004). "Partition–Edit–Count: Naive Extensional Reasoning in Judgment of Conditional Probability". Journal of Experimental Psychology 133 (4): 626–642. doi:10.1037/0096-3445.133.4.626. PMID 15584810.
- ^ a b c d e Maya Bar-Hillel and Ruma Falk (1982). "Some teasers concerning conditional probabilities". Cognition 11 (2): 109–122. doi:10.1016/0010-0277(82)90021-X. PMID 7198956.
- ^ a b c Raymond S. Nickerson (May 2004). Cognition and Chance: The Psychology of Probabilistic Reasoning. Psychology Press. ISBN 0805848991.
- ^ a b Ask Marilyn. Parade Magazine. October 13, 1991; January 5, 1992; May 26, 1996; December 1, 1996; March 30, 1997; July 27, 1997; October 19, 1997.
- ^ Tierney, John (2008-04-10). "The psychology of getting suckered". The New York Times. http://tierneylab.blogs.nytimes.com/2008/04/10/the-psychology-of-getting-suckered/. Retrieved 24 February 2009.
- ^ a b Leonard Mlodinow (2008). Pantheon. ISBN 0375424040.
- ^ Nikunj C. Oza (1993). "On The Confusion in Some Popular Probability Problems". http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.44.2448&rep=rep1&type=pdf. Retrieved 25 February 2009.
- ^ P.J. Laird et al. (1999). "Naive Probability: A Mental Model Theory of Extensional Reasoning". Psychological Review.
- ^ a b c d e f Matthew A. CARLTON and William D. STANSFIELD (2005). "Making Babies by the Flip of a Coin?". The American Statistician.
- ^ a b Charles M. Grinstead and J. Laurie Snell. "Grinstead and Snell's Introduction to Probability". The CHANCE Project. http://math.dartmouth.edu/~prob/prob/prob.pdf.